カイ二乗分布は,ここ,を参考にしました.
定義は,
標準正規分布,N(0,1)から,n個の標本,X1, X2, ... Xnを独立に抽出したとする.
この時,n個の標本の二乗和Zが従う分布を自由度nのカイ二乗分布という
というものです.
つまり,標準正規分布,
\(\Large \displaystyle X = \frac{1}{\sqrt{ 2 \pi }} \displaystyle exp \left[ - \frac{t^2}{2 } \right] \)
とした場合に,二乗和Zが,
\(\Large \displaystyle Z = X_1^2 + X_2^2 + ..... + X_n^2 = \sum_{i=1}^n X_i^2 \sim \chi (n) \)
ということです.実際の自由度nのカイ二乗分布の確率密度は,
\(\Large \displaystyle f_n (x)= \frac{1}{2^{n/2} \Gamma \left( \frac{n}{2} \right)} x^{\frac{n}{2}-1} exp \left( - \frac{x}{2} \right) \)
となるようです....すいません,式を追うことはできたのですが,しっかり身についていません...
自由度nのカイ二乗分布の確率密度とガンマ分布との関係は,ここ,に.
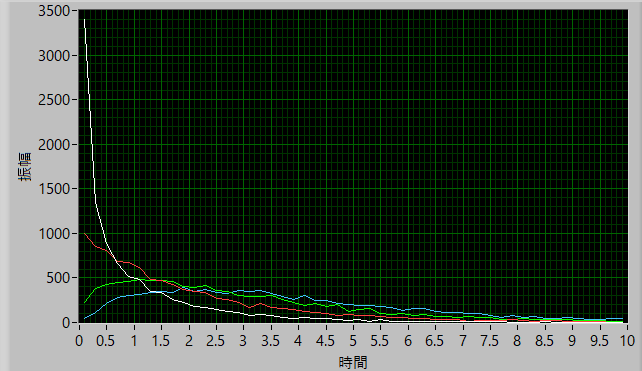
実際にシミュレートしてみると(1万回試行,n=1~4)

のように,n=1, 2, の場合は単調減少,n=3以上の場合はピークを持つ分布となります.
前頁の,
\(\Large \displaystyle U = \frac{(n-1) s^2}{ \sigma^2} = \frac{ \displaystyle \sum_{i=1}^n (x_i - \bar{x})^2}{ \sigma^2} = \chi_{n-1}^2\)
が自由度1のカイ二乗分布となることを検証しましょう.
\(\Large \displaystyle Y = \frac{ 1}{ \sigma^2} \displaystyle \sum_{i=1}^n (x_i - \bar{x})^2 \)
\(\Large \displaystyle \hspace{18 pt} = \frac{ 1}{ \sigma^2} \displaystyle \sum_{i=1}^n (x_i - \mu -\bar{x} + \mu)^2 \)
\(\Large \displaystyle \hspace{18 pt} = \frac{ 1}{ \sigma^2} \displaystyle \sum_{i=1}^n \{ (x_i - \mu) - (\bar{x} - \mu) \}^2 \)
\(\Large \displaystyle \hspace{18 pt}
= \frac{ 1}{ \sigma^2} \displaystyle \sum_{i=1}^n (x_i - \mu)^2
-\frac{ 2}{ \sigma^2} \displaystyle \sum_{i=1}^n \{(x_i - \mu) \cdot (\bar{x} - \mu) \}
+\frac{ 1}{ \sigma^2} \displaystyle \sum_{i=1}^n (\bar{x} - \mu)^2 \)
第二,三項に注目すると,
\(\Large \displaystyle
\hspace{18 pt} -\frac{ 2}{ \sigma^2} \displaystyle \sum_{i=1}^n \{(x_i - \mu) \cdot (\bar{x} - \mu) \}
+\frac{ 1}{ \sigma^2} \displaystyle \sum_{i=1}^n (\bar{x} - \mu)^2 \)
\(\Large \displaystyle
= -\frac{ 2}{ \sigma^2} (\bar{x} - \mu)\displaystyle \sum_{i=1}^n (x_i - \mu)
+\frac{ n}{ \sigma^2} (\bar{x} - \mu)^2 \)
\(\Large \displaystyle = \frac{ 1}{ \sigma^2} (\bar{x} - \mu)\displaystyle \left[ n (\bar{x} - \mu) - 2 \sum_{i=1}^n (x_i - \mu) \right] \)
\(\Large \displaystyle = \frac{ 1}{ \sigma^2} (\bar{x} - \mu)\displaystyle \left[ n (\bar{x} - \mu) - 2 n \bar{x} +2 n \mu \right] \)
\(\Large \displaystyle = \frac{ 1}{ \sigma^2} (\bar{x} - \mu)\displaystyle \left[ n (\bar{x} - \mu) - 2 n (\bar{x} - \mu) \right] \)
\(\Large \displaystyle = \frac{ 1}{ \sigma^2} (\bar{x} - \mu)\displaystyle \left[ - n (\bar{x} - \mu) \right] \)
\(\Large \displaystyle = -\frac{ n}{ \sigma^2} (\bar{x} - \mu)^2 \)
したがって,
\(\Large \displaystyle Y = \frac{ 1}{ \sigma^2} \displaystyle \sum_{i=1}^n (x_i - \bar{x})^2
= \frac{ 1}{ \sigma^2} \displaystyle \sum_{i=1}^n (x_i - \mu)^2 -\frac{ n}{ \sigma^2} (\bar{x} - \mu)^2 \)
\(\Large \displaystyle \hspace{18 pt} =\sum_{i=1}^n \frac{ \displaystyle (x_i - \mu)^2}{ \sigma^2} -\left( \frac{ \bar{x} - \mu}{ \sqrt{ \frac{\sigma^2}{n}}} \right)^2 \)
第一項は,N(0,1)の標準正規分布となるので,
\(\Large \displaystyle \sum_{i=1}^n \frac{ \displaystyle (x_i - \mu)^2}{ \sigma^2} = \chi(n) \)
となります.第二項は中心極限定理によって,標本平均Xの分布は正規分布,N(μ,σ2/n)に従うので,
\(\Large \displaystyle \left( \frac{ \bar{x} - \mu}{ \sqrt{ \frac{\sigma^2}{n}}} \right)^2 = N(0,1) = \chi(1) \)
ということで,
第一項:n個の二乗和
第二項:1個の二乗和
なので,引くと,n-1個の二乗和,となり,Yは自由度n-1のカイ二乗分布に従うことになります.
\(\Large \displaystyle \chi(n) - \chi(1) = \chi(n-1) \)
つぎは,母平均の差の信頼空間定,です.